Stanford CS229 Lecture 2.Linear Regression and Gradient Descent
Outline
- Linear Regression
- Batch/Stochastic Gradient Descent
- Normal Equation
Predict the house price
집 크기에 따라 집값을 예측하는 상황을 가정해보겠습니다.
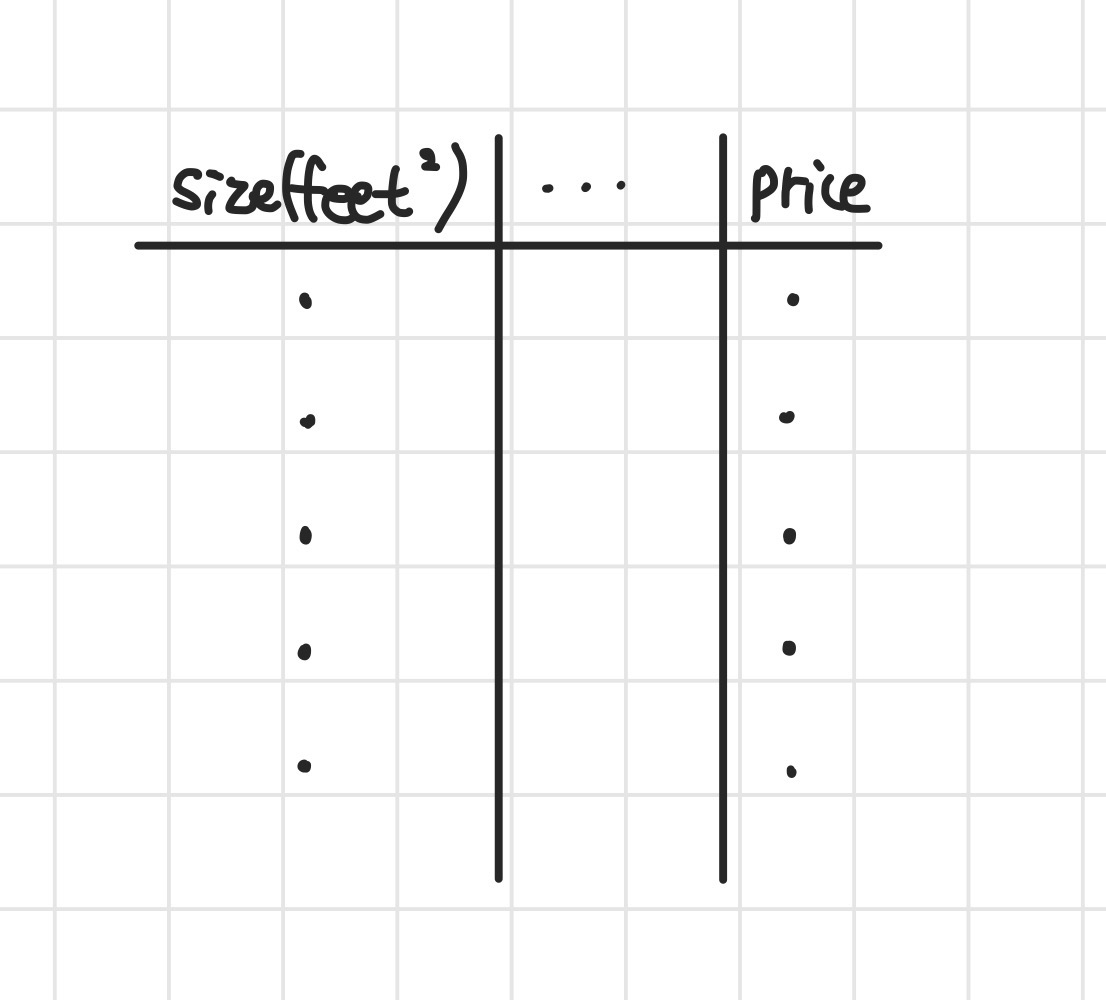
데이터는 아래 표와 같이 집의 크기와 가격이 주어집니다.
이 외에도 침실의 개수, 화장실의 개수든 다양한 feature들이 존재할 수 있습니다.
- Table
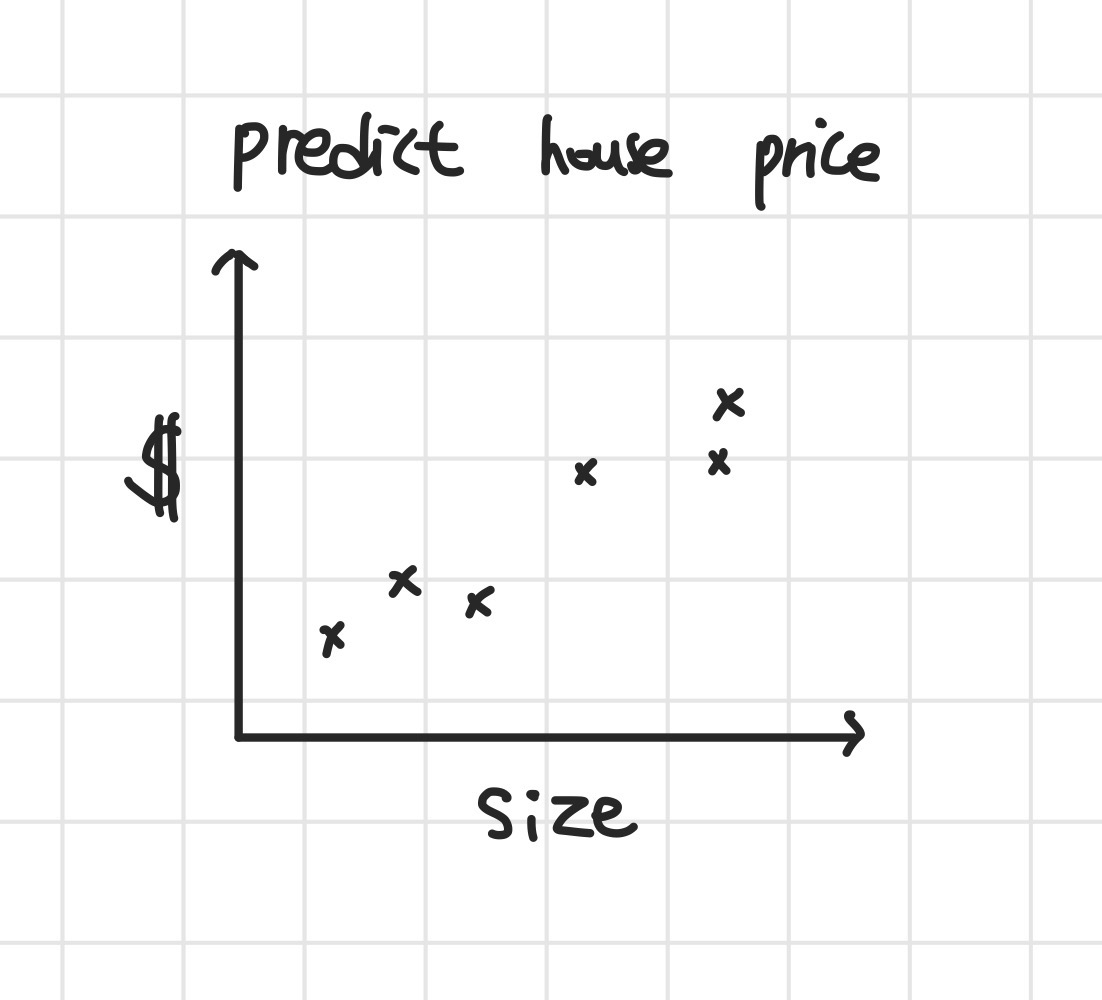
쉽게 이해하기 위해서 feature로 집의 크기(size)만 주어졌다고 가정해보겠습니다.
이를 2차원 평면에 나타내면 아래와 같이 간단하게 나타낼 수 있습니다.
- Graph
Machine Learning Process
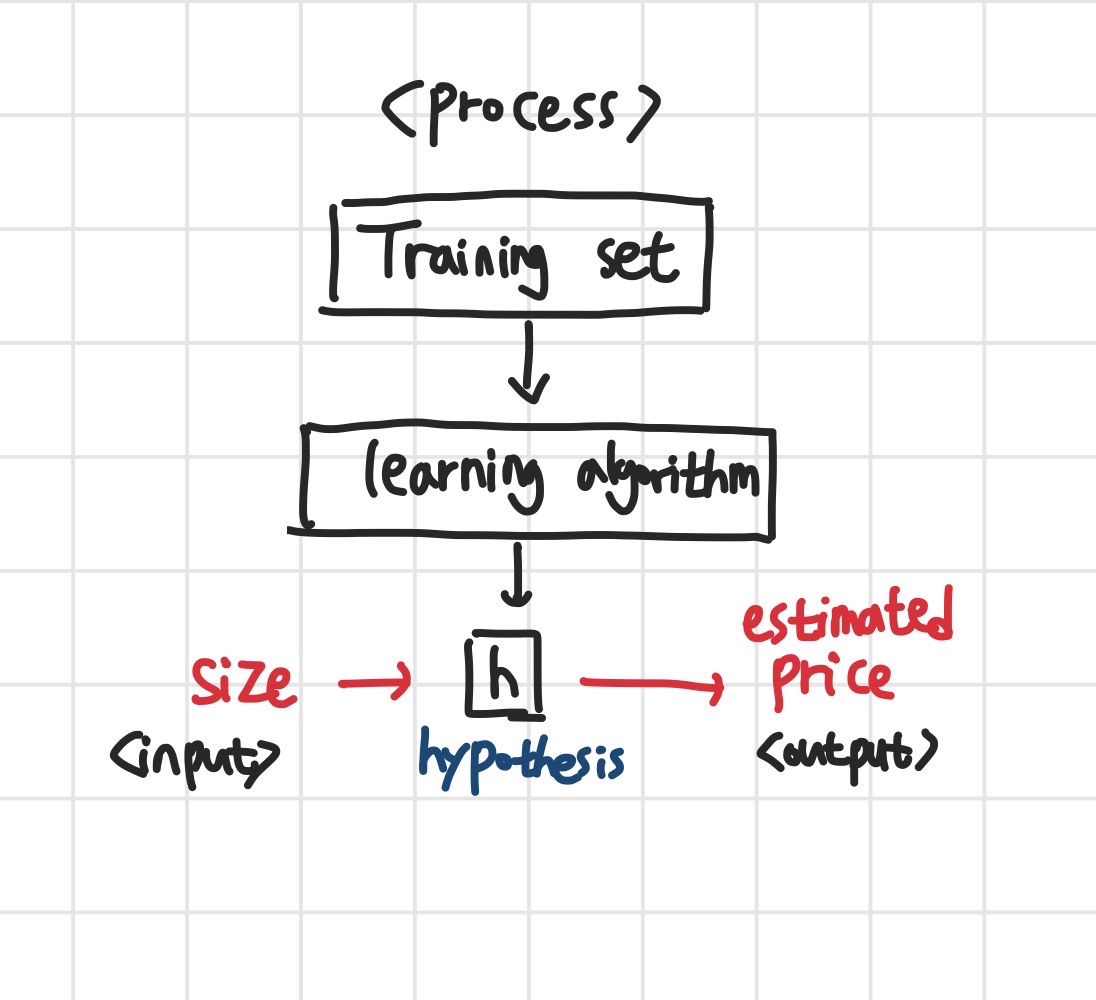
그렇다면, 위의 상황을 일반적인 머신러닝 프로세스에 대입해보면 다음과 같습니다.
- Traning set은 여러 feature가 포함된 집값 데이터 셋이 될 것입니다.
- 여기에 특정한 알고리즘을 대입합니다.
(집값을 예측하는 경우에는 Linear regression 알고리즘을 사용할 것입니다.) - 결과적으로 hypothesis(h 혹은 가설)가 도출될 것이고, 저희는 여기에 특정한 집 크기를 넣어 가장 근접한 집 가격을 도출해내는 것이 최종 목적입니다.
Notation
일반적으로, 수식에서 사용되는 표기는 다음과 같이 정의하고 있습니다.
How to represent h(hypothethis)?
그렇다면 과연 h는 어떻게 표현할 수 있는 것일까요?
- Ex) 2 features(size of the house & #bedrooms)
h는 각각의 feature에 해당하는 값을 theta에 곱한 값을 모두 더한 것으로 표현할 수 있습니다.
How to choose parameters theta?
그렇다면, 더 깊게 들어가서, 각각의 최적 theta는 어떻게 찾을 수 있을까요?
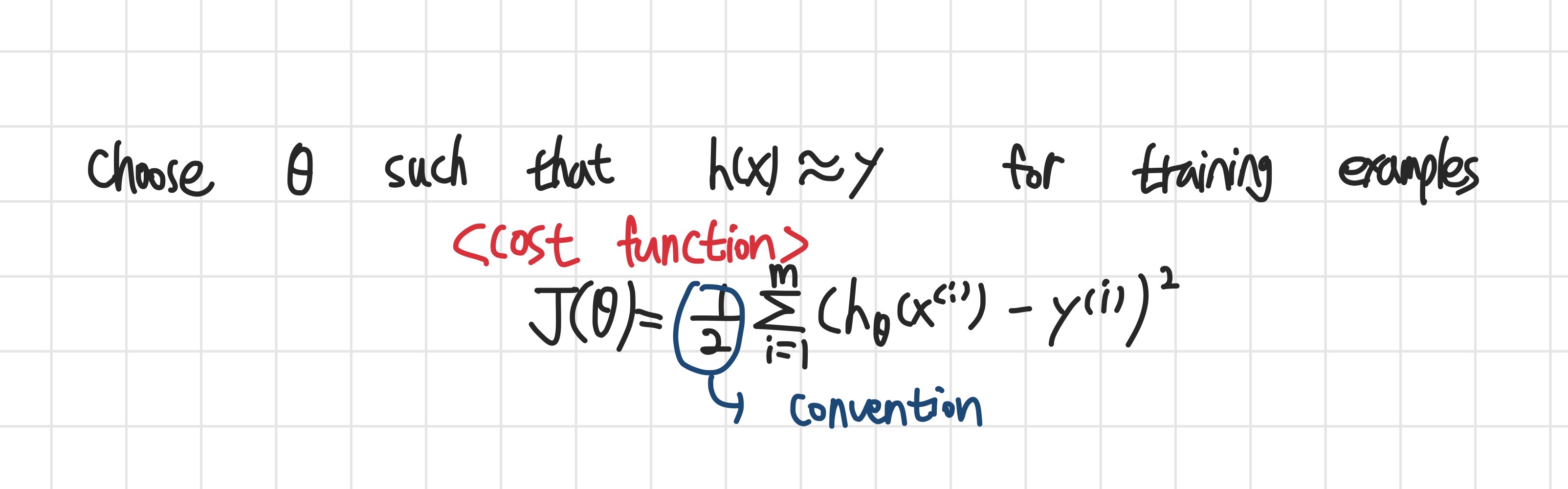
cost function은 아래의 식으로 표현할 수 있는데,
저희는 이 cost function을 최소로 만들어 줄 수 있는 theta를 찾아야 합니다.
그 해답은 Gradient Descent 즉, 경사하강법에 있습니다.
Gradient Descent
경사하강법에 대해 이해하기 쉽게 설명된 영상이 있습니다.
필요하신 분들은 아래 링크를 참고하세요.
영상:StatQuest-Gradient Descent
Start with some theta and keep changing theta to reduce J of theta
- 경사하강법은 결국 설정한 learning rate를 기반으로 step size가 결정되고,
- 각각의 theta 즉, theta 0부터 theta n까지의 값들을 변화시켜서 최솟값을 찾도록 해줍니다.
- 일반적으로 모든 데이터를 탐색하는 것을 Batch Gradient Descent라고 합니다.
- 이는 데이터가 굉장히 많을 때, 시간과 자원이 많이 필요하다는 단점을 지니고 있습니다.
- 그래서 Stochastic Gradient Descent를 활용하는 경우가 많습니다.
Stochastic Gradient Descent
이는 전체 데이터를 탐색하는 것이 아니라, 특정 데이터에 맞춰서 연산을 수행합니다.
여러 데이터 중 하나를 골라, theta 값을 결정하고, 다른 데이터를 골라 theta 값을 수정합니다.
위 과정을 반복하면서 최솟값을 찾는데, 이 방법을 활용할 경우, global minimum 값에는 수렴할 수 없습니다.
하지만, 이 결과값이 유의미한 이유는, 도출된 theta만으로도 충분히 예측력이 높고, global minimum과 근소한 차이만 보이기 때문입니다.
Normal Equation
정규표현식은 한번만에 최적의 local minimum을 찾도록 하는 방법입니다. 수학적 풀이는 lecture note를 참고하시면 좋습니다.
Summary
1강에서는 크게 Linear Regression의 원리에 대해서 배웠습니다. hypothesis -> cost function -> gradient descent로 이어지는 매우 중요한 기초를 배웠습니다.
주로, 벡터, 행렬, 편미분이 활용되고 수학적 이해가 완벽히 되지는 않았지만,
이전에는 단순히 선형회귀식이 각각의 데이터와의 거리를 최소화하는 것이라고만 모호하게 알고 있었던 것에 반해,
이번 강의를 통해 hypothesis를 기반으로 한 cost function을 최소화하는 것이라고 구체적으로 알게 되었고,
linear regression 뿐 아니라, clustering, deep learning에 이르기까지 많이 활용될 수 있는 gradient descent의 원리를
이전보다 이해하고 넘어갈 수 있게 되었습니다.
데이터, 그래프, 수식 등 lecture note에 구체적으로 서술되어 있기 때문에 꼭 활용하시는 것을 권장드립니다.
혹시 잘못된 설명이나 댓글 달고 싶은게 있으시다면 아래에 편하게 달아주세요.
Just do it & Keep steady


댓글남기기