Stanford CS229 Lecture 3.Locally weighted & Logistic Regression

Outline

1. Locally weighted Regression
2. Probabilistic interpretation
3. Logistic Regression
4. Newton’s method

---

Locally weighted Regression

Locally weighted regression(국소가중회귀)는 데이터가 선형회귀식에 들어맞지 않을 때 사용하는
회귀식이다. (when the data does not fit in straight line)

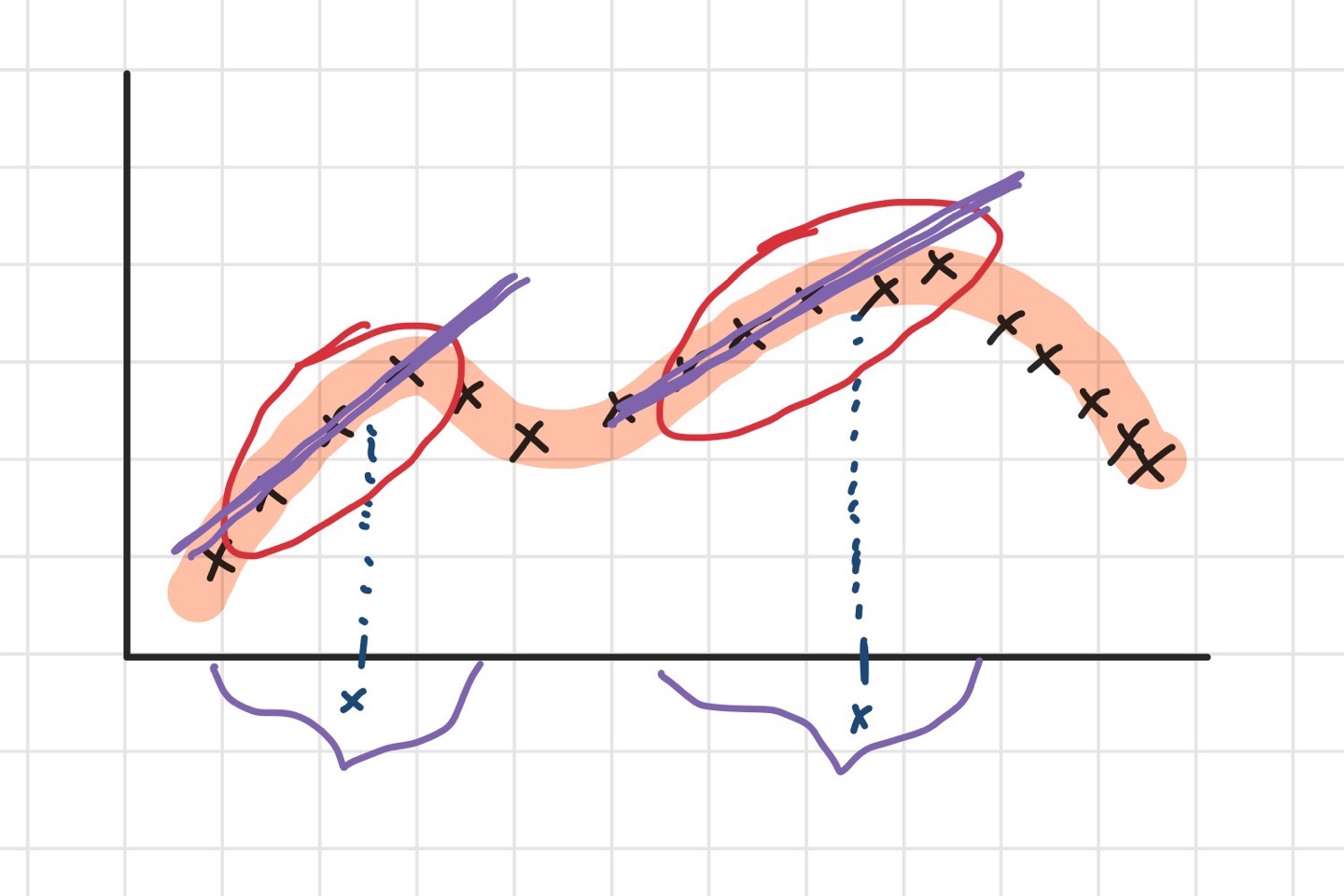위의 그래프와 같이 데이터가 존재한다고 할 때, 선형회귀의 경우, 최적의 theta를 구해서
데이터를 가로지르는 회귀선을 그려서 원하는 x에 대한 y값을 예측했을 것입니다.
하지만, LWR에서는 원하는 x와 인접한 데이터만을 탐색해서 설정한 폭만큼의 데이터에 대한 선형회귀를
적용하는 것입니다.
t 모양의 tau(타우)는 hyperparameter로서, tau값을 어떻게 설정하냐에 따라 bandwidth가 달라지게 됩니다.

Parametric vs Non-parametric

• Parametric model : Fit Fixed set of parameters theta
• Non-parametric model : Amount of data/parameters you need to keep grows (linearly) with size of data
  • LWR is non-parametric model and it need high memory
    • => LWR can be good choice when features are two or three

---

Logistic Regression

로지스틱 회귀는 대표적으로 Classification 문제를 해결하는데 사용할 수 있습니다.
0과 1, 양성과 음성 등 이진 분류에 자주 활용됩니다.

앞서, 선형회귀의 확률적 해석에 기반하면, MLE(Maximum likelihood estimation)는 가능도를
최대화시켜주는 theta를 고르는 것이 목적이었는데, 이는 결국 선형회귀에서 등장한
J of theta, 즉 cost function을 minimize 해주는 theta를 구하는 것과 같다는 증명이 강의노트에 등장합니다.
이를 토대로 보았을 때, logistic regression에서는 batch gradient ascent를 통해 theta를 구할 수 있습니다.

---

Newton’s method

gradient ascent보다 훨씬 빠르지만, 비용이 많이 드는 방법입니다. 몇 번의 반복만 거쳐도 error가 빠르게 수렴하여 f의 theta가 0과 매우 근접하게 수렴하게 할 수 있습니다.
강의에서는 10개~50개의 feature가 존재할 때는 이 방법을 추천하고, 그보다 많은 경우에는 gradient ascent의
사용을 추천합니다.

그 이유는 newton’s method의 경우, Hessian matrix의 역행렬이 (n+1) * (n+1)의 크기를 가지기 때문입니다.

이번 강의에서는 수식이 많이 등장하기 때문에 별도로 업로드하진 않지만 강의노트를 참고하고,
2강부터 배웠던 Linear regression -> Probabilistic interpretation -> Logistic regression으로 이어지는
흐름을 파악하는 것이 중요해보입니다.

데이터, 그래프, 수식 등 lecture note에 구체적으로 서술되어 있기 때문에 꼭 활용하시는 것을 권장드립니다. 혹시 잘못된 설명이나 댓글 달고 싶은게 있으시다면 아래에 편하게 달아주세요.

Just do it & Keep steady