모두를 위한 딥러닝 Lec 02, 03 Linear regression

Lec 02, 03 Linear Regression & cost function

Hypothesis

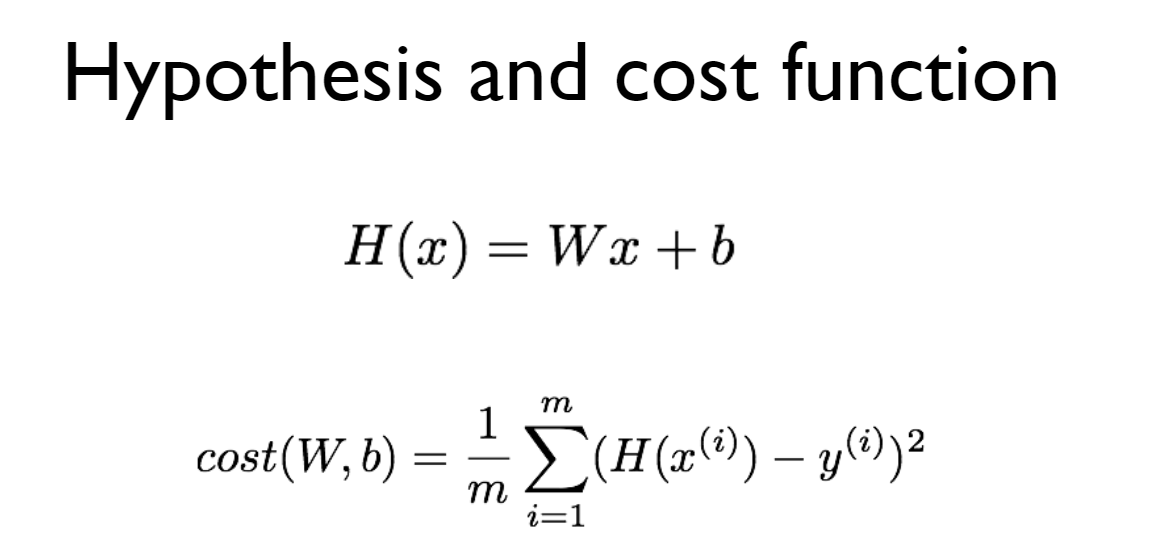
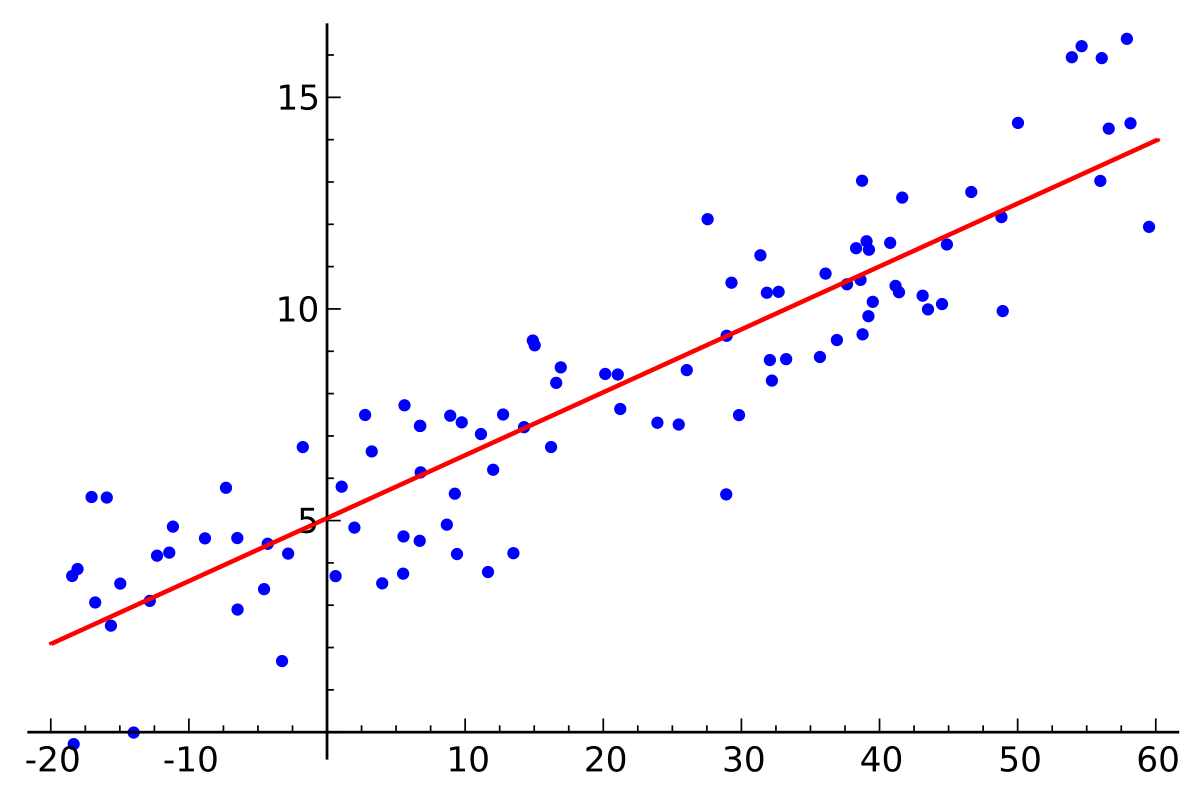
여기서 여러 관측값과 하나의 직선 사이의 거리의 합이 최솟값이 될 수 있는

아래 그림처럼 cost는 실제 값과 직선 사이의 거리를 제곱한 것의 평균을 나타낸다.

영상에선 hypothesis를 좀 더 간단하게 만들었다.

Simplify

---

우리는 이 직선을 어떻게 찾을 수 있을까?

해답은 Gradient Descent이다.

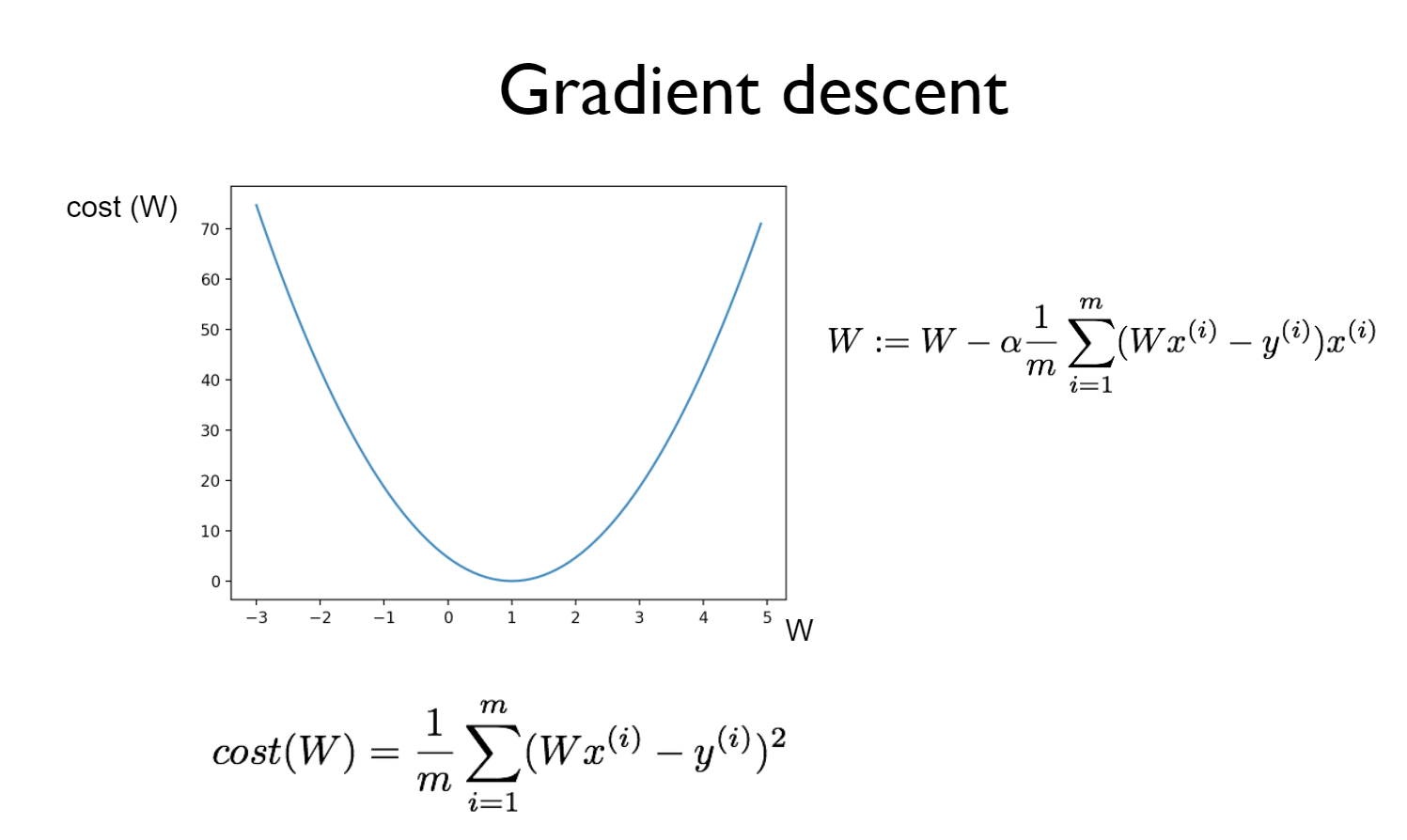
위의 hypothesis를 가지고 예를 들자면, 직선과 값들의 cost는 W가 1이 될 때,

최솟값을 가지게 된다. 이처럼, 직선 상의 어떤 점에서 시작하더라도, 그것이 기울기가 0으로 수렴하게끔 하는 원리로 우리는 W를 구할 수 있고, 이것이 cost minimization이 된다.

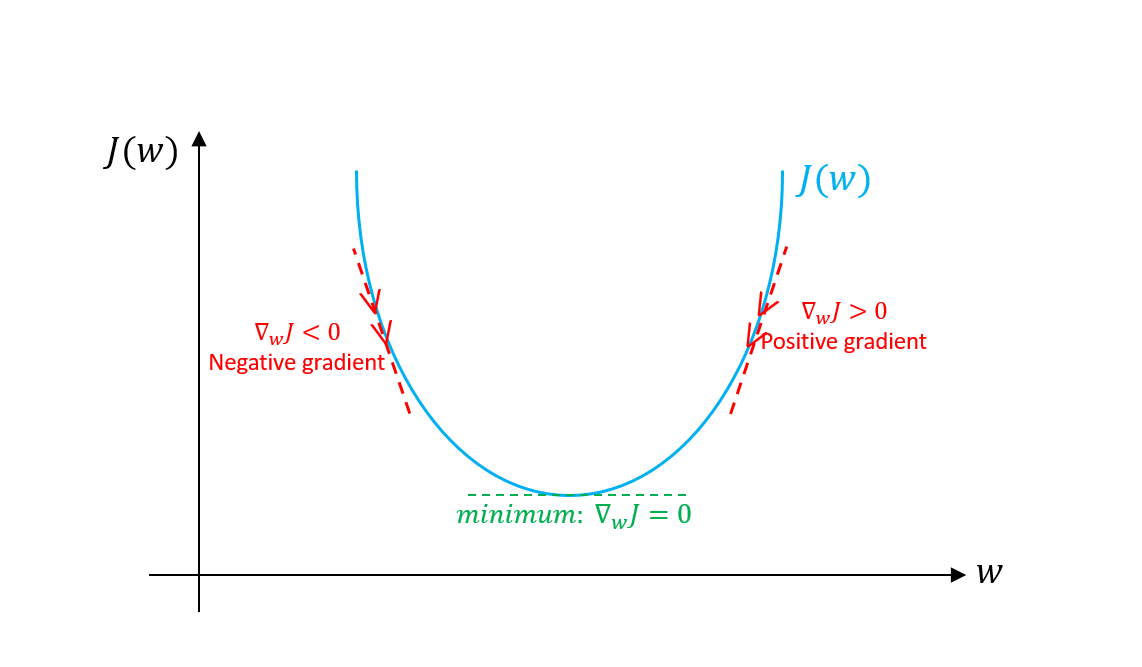
추가적인 설명을 하자면 기울기가 0보다 클 경우, 알파의 - 값을 통해 기울기가 점점 작아지게 할 수 있고, 반대로 음수일 경우엔, -를 통해 양수쪽으로 옮겨갈 수 있다.

#주의할 점

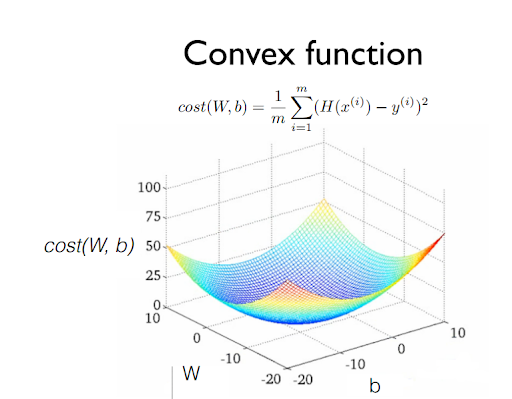
주의할 점은 Cost function을 설계할 때, 반드시 이 모양이 Convex function이 되는지를 확인해야 한다.

Convex function일 경우에 어느 점에서 시작하더라도 최솟값이 하나를 가질 수 있지만, 그렇지 않은 경우엔 여러 값들이 나올 수 있기 때문이다.