KMOOC 통계학의 이해1 10주차-1
포아송분포(Poisson distribution)
- 이항분포에서 n이 커지면 계산하는데 어려움
- p가 작은 경우(0 근처에 있는 경우)
- p가 큰 경우(1 근처에 있는 경우)
- p가 0.5에서 멀리 떨어져 있지 않은 경우
- X ~ B(n,p)
- p가 매우 작으면 큰 x에 대한 확률은 무시할 정도로 작음
- p가 매우 작으면 큰 x에 대한 확률은 무시할 정도로 작음
- 구간을 나눴을 때 각 구간의 발생 빈도는 서로 독립(independent increment)
- 구간의 위치와 관계없이 동일 길이의 구간에서의 평균발생빈도는 동일(stationary increment)
X : 위의 상황에서 해당 사건이 일어날 횟수
- X ~ Pois(람다)
- 람다에 따라 분포의 형태가 달라짐 => 람다 = 모수(parameter)라고 부름
포아송분포의 성질
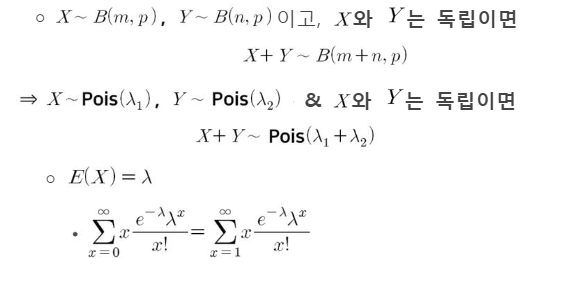
사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.


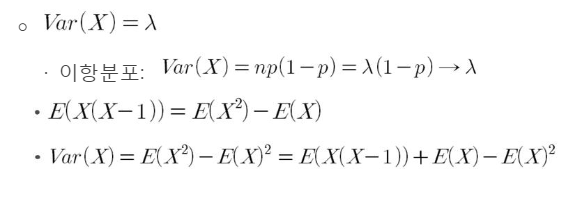
댓글남기기