KMOOC 통계학의 이해1 11주차-3
확률표본과 통계량
확률표본(random sample)
- 모집단에서 무작위로 선택되어진 관측값
- 서로 독립이고 동일한 분포를 따른다고 가정
- Independently and Identically Distributed(IID)
- (독립, 동일한 분포) => 복원추출
- 예 : 정규분포에서 추출한 경우
- 독립이기 때문에 결합분포는 각각의 주변분포 곱으로 표시
- 동일한 분포를 따르기 때문에 동일한 확률질량(밀도)함수를 가짐
- X1, X2, …, Xn이 확률표본이고 Xi ~ f(x)이면
통계학적 관점에서 표본을 뽑는 이유
- 모집단에 대한 추론
- 통계량(statistic): 관측가능한 표본의 함수
- 관측가능하다는 것은 미지의 모수를 포함하지 않음을 의미
- 추정량(estimator): 모수의 추정에서 사용되는 통계량
- 확률변수
- 추정값(estimate, 추정치): 추정량의 관측값
- 확률분포가 다음과 같을 때
| x | 0 | 1 | 2 |
|---|---|---|---|
| P(X=x) | 2/5 | 2/5 | 1/5 |
- 두 개의 확률표본 추출: X1, X2
- Y = max(X1,X2)일 때 Y의 분포는?
| x | 0 | 1 | 2 |
| 0 | 4/25 | 4/25 | 2/25 |
| 1 | 4/25 | 4/25 | 2/25 |
| 2 | 2/25 | 2/25 | 1/25 |
- 0,1,2이 교차하는 영역을 각각 더 해주면 y에 대한 확률분포를 구할 수 있다.
| y | 0 | 1 | 2 |
|---|---|---|---|
| P(Y=y) | 4/25 | 12/25 | 9/25 |
- 통계량의 확률분포 => 표집분포(sampling distribution)
- 표본이 아닌 모집단에 관한 것이라는 것을 명심
사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.

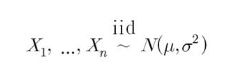
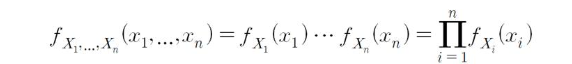
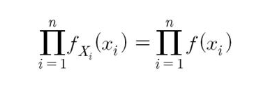



댓글남기기