KMOOC 통계학의 이해1 3주차-1

수치를 이용한 자료정리

중심위치

• 가장 많이 사용되는 중심위치 통계값은 평균

표본평균(sample mean)

• 표본평균은 표본의 합을 표본크기로 나눈 값
  

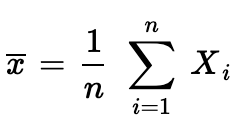
• 평균은 무게중심과도 같고, 편차(deviation)의 합은 0이다.

표본비율(sample proportion)

• i번째 관측값이 어떤 범주에 속하면 xi의 값을 1, 속하지 않으면 0으로 표시
• 표본비율 = 표본평균

이상점(outlier)

• 대부분의 관측값으로부터 멀리 떨어져 있는 일부 관측 값
• 이상점의 포함 여부에 따라 표본평균의 값에 차이가 크게 나는 경향이 있음
  => 이상점에 robust하지 않음
• 대체 통계값 : 중앙값, 절사 평균, 최빈값 등

가중평균(weighted mean)

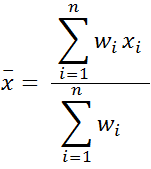
• 예 : A 상품 700 투자 -> 28% 이익 / B 상품 300 투자 -> 28% 손실
  • 수익 = 700 * 0.28 + 300 * (-0.28) = 112
  • (평균수익률) = 112/(700+300) = 0.112 = 11.2%

기하평균(geometric mean)

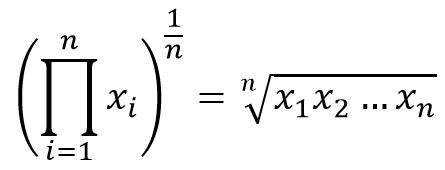
• 예 : 1인당 총소득 1985년 209만원, 2015년 3093.5만원이라고 할 때
  연평균 증가율
  • 3093.5/209 = 14.80 = (1+R)**30
  • 1+R = 14.8**1/30 = 1.094 => R = 0.094(9.4%)

조화평균(harmonic mean)

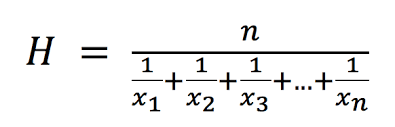
• 예 : 절반을 60km/h 로 달리고, 나머지 절반을 40km/h 로 달렸을 때 평균 속력
  • 절반 거리 = y 걸린 시간 = (t1,t2) 라 할 때,
  • 평균속력 = 2y/t1+t2 = 2y/(y/60 + y/40) = 48km/h

  사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.