KMOOC 통계학의 이해1 3주차-3

수치자료 분포의 산포1

산포(dispersion, 퍼짐)

• 자료들이 얼마나 퍼져 있는지를 나타내는 측도
• 중심위치가 얼마나 안정적인지에 대한 중요한 정보를 제공

1. 범위(Range)

• 자료 중 가장 큰 값과 작은 값의 차이
• 최대값과 최소값에만 영향을 받기 때문에 자료 전체의 퍼져 있는 정도를 파악할 수 없다.

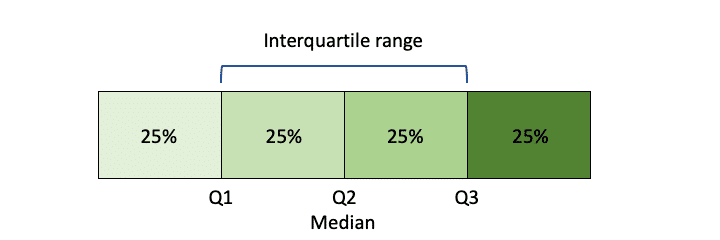
2. 사분위(간)범위(Interquartile-Range)

• 사분위수(quartile) : 자료를 동일한 비율로 4등분 할 때의 세 위치
  • 자료를 오름차순으로 정렬할 때
    • 25% 지점 : 제1사분위수(Q1)
    • 50% 지점 : 제2사분위수(Q2)
    • 75% 지점 : 제3사분위수(Q3)
• 사분위(간)범위는 제3사분위수와 제1사분위수의 차이
  

사분위수 계산 방법

• k = (n-1)p+1, p = 0.25, 0.5, 0.75
• k가 정수이면 x(k)가 해당 사분위수이고, 아니면 비례에 의한 내삽법을 적용
  • 예 : n = 41
    • k = 40 * 0.25 + 1 = 11 => Q1 = x(11)
    • k = 40 * 0.5 + 1 = 21 => Q2 = x(21)
    • k = 40 * 0.75 + 1 = 31 => Q3 = x(31)

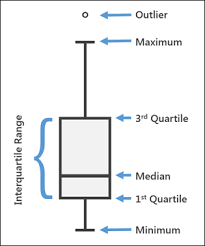
상자그림(boxplot)

• 통계학자 Tukey에 의해 제안된 그림
• 자료의 주요 위치 파악과 이상점 검출 등에 사용
• Q1,Q2,Q3을 계산하여 직사각형의 상자를 표시
• L = Q1 - 1.5IQR, U = Q3 + 1.5IQR 계산
  • L보다 작거나 U보다 큰 값은 이상점으로 표시
  • L보다 큰 관측값 중 가장 작은 값, U보다 작은 관측값 중 가장 큰 값 직선으로 표시하고, 상자와 연결
    

사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.