KMOOC 통계학의 이해1 3주차-4
수치자료 분포의 산포2
표본분산과 표본표준편차
- 모든 자료들 간의 거리의 합 이용 방법? 거리(distance)
- 모든 관측값들 간 거리의 합
- 자료들이 넓게 퍼져있으면 이 값이 커지고, 모여있으면 작아짐
- 중심위치 a와 모든 관측값들 간 거리의 합 : a를 어떻게 선택할 수 있을까?
- a가 좋은 중심위치가 되려면 자료들 간 거리가 가능한 짧아야 함 => 거리의 합을 최소로 만드는 값
- 퍼져있는 정도를 나타내는 통계값
표본분산(sample variance)
- 표본분산은 n개의 편차를 사용하는 것 같지만 n-1개의 편차정보를 사용
- n-1: 자유도(degree of freedom)
- 이 부분에 대해서 여기를 확인하면 추가적인 이해가 쉬울 것 같다.
수학적으로 추가적인 이해력이 요구된다.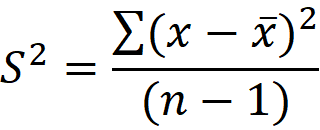
표본표준편차(sample standard deviation)
- 표본분산은 편차의 제곱합을 이용하기 때문에 분산의 단위는 관측값 단위의 제곱
- 눈으로 이해하는 산포와 일치하기 위해서는 자료를 측정할 때의 단위로 표시
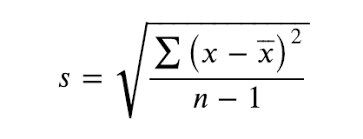
표준화(standarization)
- 표준화된 자료의 평균과 분산
- 평균 0, 표준편차 1 => 측정 단위에 영향을 받지 않게 중심위치와 척도를 조정해 절대비교 가능
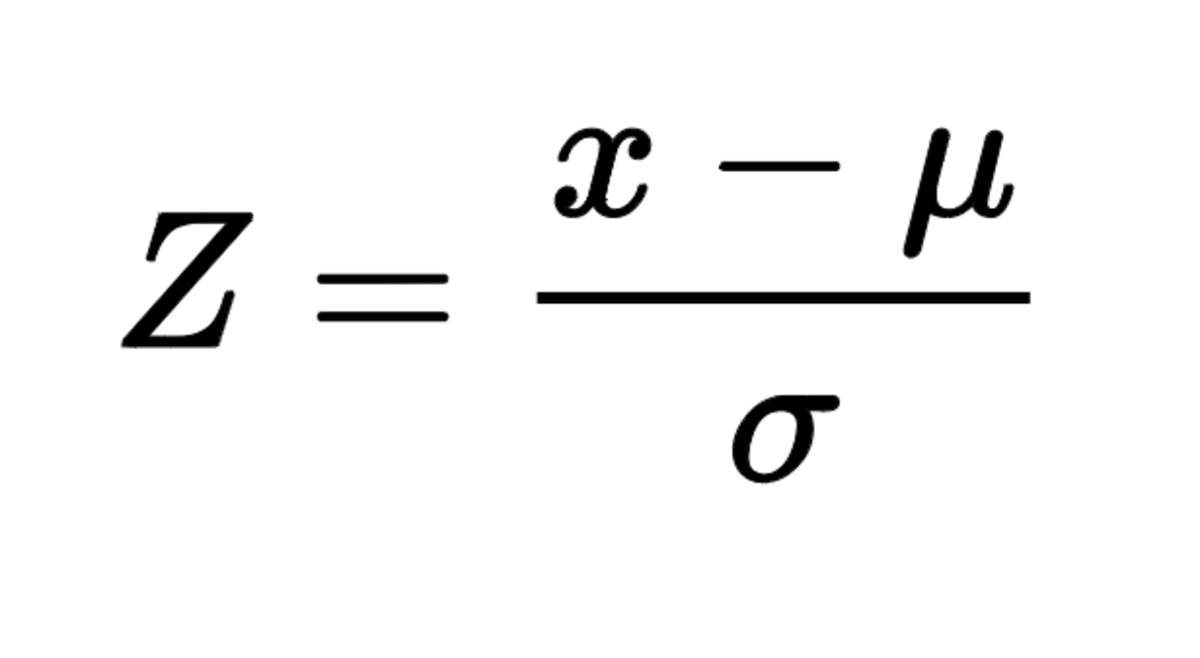
변동계수(coefficient of variation)
- 표준편차가 평균에 영향을 받는 경우
- 표준편차만 이용하여 산포를 비교하는 것은 적절하지 않을 수 있어 평균으로 표준편차를 보정
- 100을 곱해서 표본평균에 비해 표본표준편차가 얼마나 큰지를 % 개념으로 표시하기도 함
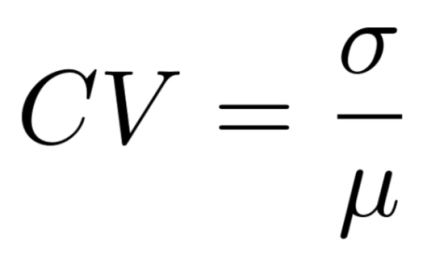
- 100을 곱해서 표본평균에 비해 표본표준편차가 얼마나 큰지를 % 개념으로 표시하기도 함
사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.

댓글남기기