KMOOC 통계학의 이해1 4주차-3
공분산과 상관계수
- 산점도 : 두 수치변수 간에 관계가 있는지를 시각적으로 확인
- 두 수치변수 간에 직선관계가 어느 정도인지를 나타내는 통계값
-
자료표시 : (x1,y1), (x2,y2),…,(xn,yn)
-
양과 음의 관계를 가지는 산점도
- 고려사항
- 위치에 따라 직선관계에는 변화가 없음
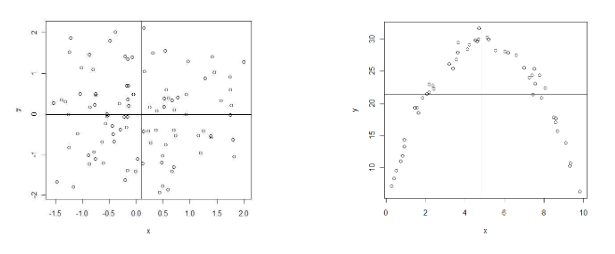
- 좌 그림: 평균을 중심으로 1과 3사분면에 자료가 많고 길게 분포 => 음수로 표시
- 평균에서 멀어질수록 직선관계가 명확해짐
- 고려사항
표본공분산(sample covariance)
- 좌 그림 : 양의 기울기인 선분에 자료가 모여 있음 => c > 0
- 우 그림 : 음의 기울기인 선분에 자료가 모여 있음 => c < 0
-
yi를 xi로 바꾸면
=> 분산(하나의 변수 x) -
직선관계가 없는 산점도(c가 0에 근접)
- 표본공분산의 간편식
표본상관계수(coefficient of correlation)
- 표본공분산의 문제점
- 측정 단위에 영향을 받기 때문에 그 값 자체로 선형관계의 정도를 알 수 없음
- 예 : 우승기록을 초 => 분 단위로 표시
- 남자 표본공분산 : -13.98 => -0.233
- 측정 단위에 영향을 받기 때문에 그 값 자체로 선형관계의 정도를 알 수 없음
- 피어슨의 표본상관계수
- 표준화된 자료의 표본공분산
- 표준화된 자료의 표본공분산
- 표본상관계수의 간편식
- Cauchy-Schwartz 부등식 :
=> -1 <= r <= 1
- Cauchy-Schwartz 부등식 :
- 표본상관계수의 성질
- 기울기를 가지는 직선에 조밀하게 모일수록 절댓값 r은 1에 근접
- 모든 관측값들이 직선 위에 위치하면 절댓값 r = 1
- r이 음수이면 음의 상관관계가 존재
- r이 양수이면 양의 상관관계가 존재
- 절댓값 r이 0에 근접하면 상관관계가 없다고 함 => 직선관계가 없다는 것을 의미
- 어떤 관계도 존재하지 않는다는 것은 아님
- 절댓값 r이 얼마 이상이어야 상관관계가 있다고 할 수 있는지?
=> 통계학의 이해2
- 기울기를 가지는 직선에 조밀하게 모일수록 절댓값 r은 1에 근접
상관관계 사용 시 주의할 점
- 두 변수 간에 직선관계가 있는지를 나타낼 뿐 인과관계를 나타내는 것은 아님
- 예 : 휴대전화 보급률과 기대수명에 대한 상관계수
- 매우 높은 양의 상관관계를 가짐
=> 기대수명을 늘리기 위해 휴대전화 보급을 늘려야 한다? X
- 매우 높은 양의 상관관계를 가짐
- 잠복변수(lurking variable) : 두 변수에 영향을 주는 변수
- 연도에 따라 보급률 증가, 기대수명 증가
=> 허위상관(spurious correlation) - 보급률과 기대수명에서 연도의 영향력을 제거하고 상관관계유도
- 연도에 따라 보급률 증가, 기대수명 증가
- 예 : 휴대전화 보급률과 기대수명에 대한 상관계수
사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.


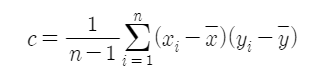
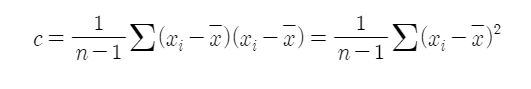
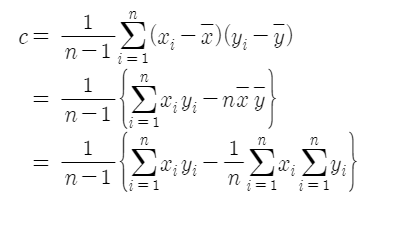
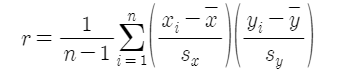
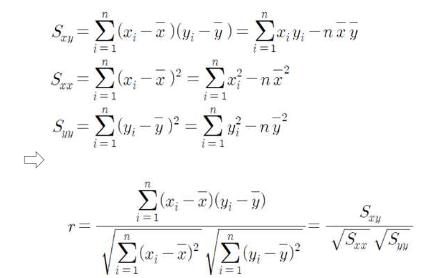
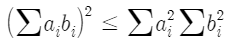
댓글남기기