KMOOC 통계학의 이해1 5주차-1
확률이란
확률(probability)
- 어떤 사건이 발생할 가능성이 얼마나 되는지를 나타내는 [0,1]의 수치적 측도
- 확률을 언급하기 위해서는 확률실험이 전제
=> 표본공간과 사건이 설정되어야 함
- 확률을 언급하기 위해서는 확률실험이 전제
확률실험(random experiment)
- 실험을 시행하기 전에 발생할 수 있는 모든 결과는 알 수 있음
- 실험을 하기 전까지 이들 결과 중 어떤 것이 발생할 것인지에 대해 확실하게 예측할 수 없음
=> 불확실성 - 위의 두 성질을 가지는 실험
표본공간(sample space)
- 확률실험에서 발생 가능한 모든 결과들의 집합
사건(event)
- 표본공간 내에서의 관심 부분집합
고전적 확률
가정
- 표본공간의 각 원소(근원사건)의 발생가능성이 동일(equally likely)
- n : 표본공간의 원소개수
- k : 사건 A의 원소개수
- 사건 A의 확률
연속표본공간
- 발생가능성이 동일한 상황을 선이나 평면 등을 이용
- 사건 A가 발생한다는 것은, 표본공간 내에서 무작위로 한 점을
선택할 때 이 점이 영역 A에 있다는 의미 - 사건 A의 확률은 전체 영역에서 A가 차지하는 비율
사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.

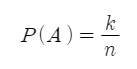

댓글남기기