KMOOC 통계학의 이해1 7주차-1

확률변수란?

확률변수(random variable)

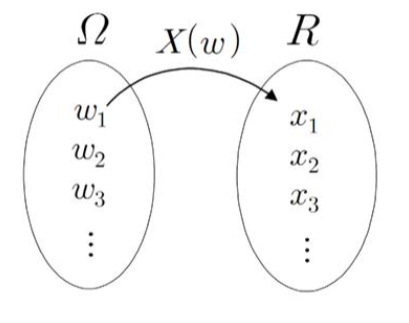
• 표본공간에서 정의된 실함수(real-valued function)
• 정의역이 표본공간이고 공역이 실수인 함수 => 확률실험 + 불확실성
  
• 표본공간을 숫자로 표시하고 불확실한 현상을 수학적으로 모형화
  • 불확실성을 제거하는 것이 아니고, 구체적으로 계량화된 분석을 할 수 있음
• 확률변수는 대문자 X,Y,Z 등으로 표시하며 확률변수의 값은 소문자 x,y,z 등으로 표시

이산확률변수(discrete random variable)

• 확률변수가 가질 수 있는 값들이 가산(countable) 또는 셀 수 있는 경우
  • 예 : 불량품의 개수, 사고건수, …

연속확률변수(continous random variable)

• 가질 수 있는 값이 셀 수 없을 정도로 많은 경우
  • 예 : 수명, 신장, 체중

확률분포(probability distribution) => [0,1]

• 확률변수의 값에 대해 확률을 표시한 것
  
• 확률변수는 표본공간의 값을 숫자로 바꾼 함수
  • 확률변수가 어떤 값을 가진다는 것은 표본공간 내에 대응하는 원소들이 존재
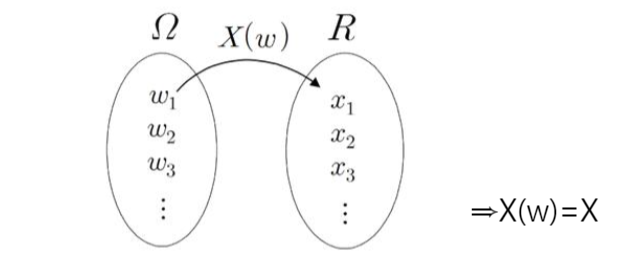
• 수식표현
  
  • 확률변수에 대해 X=x 또는 a <= X <= b에 대응하는 확률을 계산할 수 있음
• 확률변수는 숫자로 표시되고 해당 숫자에 대한 확률을 구할 수 있음
• 확률변수의 값에 따라 확률이 어떤 형태로 분포되어 있다는 말을 할 수 있음

확률분포표(probability distirbution table)

• 확률변수의 확률을 표로 표시한 것

---

• 확률은 모집단이 어떤 형태로 이루어져 있는지를 보여줌
  => 확률분포는 모집단을 숫자로 표시했을 때의 형태 = 모집단의 확률구조

모집단의 확률구조를 표시하는 방법

• 이산확률변수 : 확률질량함수, 누적분포함수, …
• 연속확률변수 : 확률밀도함수, 누적분포함수, …

사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.