이산확률변수와 확률질량함수
확률질량함수(probability mass function)
- 이산확률변수 : 확률변수의 치역이 셀 수 있는 경우
- 이산확률변수 X가 임의의 값 x일 확률 = P(X=x)
- 예 : 젖혀진 윷이 나올 때까지 던지기
- X : 던진 횟수, p : 젖혀질 확률
f(1) = P(X=1) = P({S}) = p
f(2) = P(X=2) = P({FS}) = (1-p)p
f(3) = P(X=3) = P({FFS}) = (1-p)^2*p
=> f(x) = p(1-p)^(x-1)
- 기하분포(geometric distribution)
- 확률질량함수의 성질

누적분포함수(cumulative distribution function)
- 성질 3의 특수한 형태
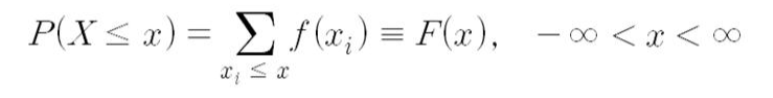
- 확률변수의 변환(함수) => 확률변수의 함수도 확률변수
- 변환된 확률변수의 확률분포 유도 가능
- X의 확률변수
| x |
-1 |
0 |
1 |
2 |
| P(X=x) |
0.1 |
0.3 |
0.2 |
0.4 |
- P(W=0) = 0.3
- P(W=1) = 0.1 + 0.2 = 0.3
- P(W=4) = 0.4
사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.


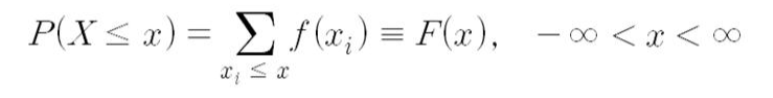
댓글남기기