KMOOC 통계학의 이해1 7주차-3
연속확률변수와 확률밀도함수
확률밀도함수(probability density function)
- 연속확률변수 : 확률변수의 치역이 실수
- 히스토그램
- 밀도(density) : 히스토그램의 높이
- 전체 면적 = 1
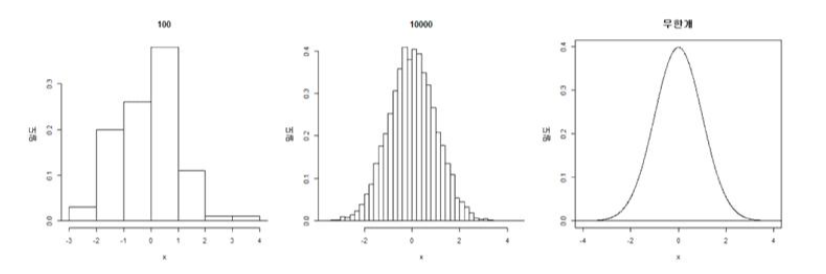
- 연속자료로 이루어진 모집단에서 표본추출
- n =100, 1000 => 표본
- n이 무한대로 가면 모집단 : x에서의 높이(밀도) = f(x) => 확률밀도함수
0~12까지의 숫자가 표시된 돌림판
- 표본공간 = {x: 0< x <= 12}
- X : 바늘이 지적하는 위치
- 0에서 12사이에서 발생가능성이 동일
=> 밀도는 이 구간에서 동일 : f(x) = c
확률밀도함수에서의 확률
- 히스토그램의 면적 = 해당 구간에서의 비율(상대도수)
- 확률밀도함수의 면적 = 해당 구간에서의 확률
- X가 구간 [a,b]에 속할 확률:
- 0~12까지의 숫자가 표시된 돌림판
- X가 3에서 6사이에 있을 확률
P(3<= X <= 6) = 3/12 = 1/4
- X가 3에서 6사이에 있을 확률
- Q : X=3 일 확률은? P(X = 3) = 0
연속확률변수에서는 항상 면적으로 표현한다. 특정 점에 대해선 0의 값을 가짐 - X가 연속확률변수일 때
- 모든 x에 대해 P(X=x) = 0
- P(a < X < b) = P(a < X <= b) = P(a <= X < b) = P(a<= X <= b)
- 확률밀도함수 f(x)는 x에서의 확률이 아니라 그 위치에서 상대적으로 얼마나 밀집되어 있는지를 나타낸 것
- 확률밀도함수의 성질
누적분포함수(cumulative distribution function)
- 성질 3의 특수한 형태
- 예 :
사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.

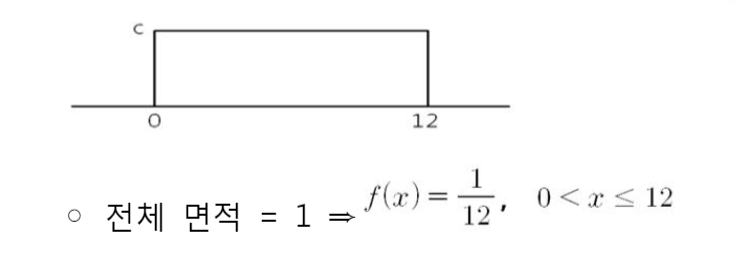
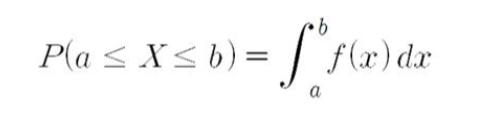
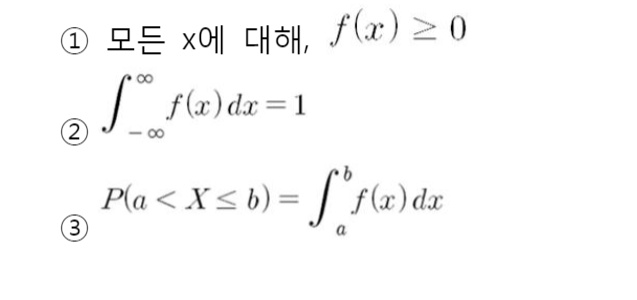
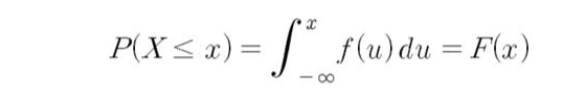

댓글남기기