KMOOC 통계학의 이해1 7주차-4
확률변수의 기댓값
기댓값(expectation, expected value)
표본평균
- {1,2,3,4,5,6}으로 이루어진 모집단으로부터 5개의 표본을 무작위로 선택 : 1,1,2,5,6
- 표본평균 = (1+1+2+5+6)/5 = 3
=> 관측된 값에 자료 중 그 값이 차지하는 비율을 곱하여 더한 것으로 표시 - 표본크기 n이 계속 커지면 표본 => 모집단, 표본평균 => 모평균(뮤)
- 확률변수의 기댓값(expected value)
- 확률변수에 대해 평균적으로 기대하는 값 = 모평균(population mean)
=> 확률분포(또는 모집단)의 무게중심 - 이산확률변수 X의 기댓값 계산
- 연속확률변수의 기댓값(시그마 => integral)
=> f(x)dx = 확률밀도함수 X 단위길이(높이)
- 확률변수에 대해 평균적으로 기대하는 값 = 모평균(population mean)
기댓값의 성질
사진과 글은 KMOOC 사이트에서 숙명여대의 여인권 교수님의 [통계학의 이해1] 수업자료를 바탕으로 했습니다.


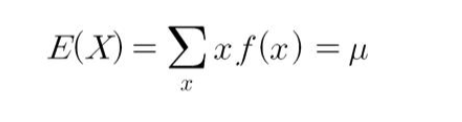
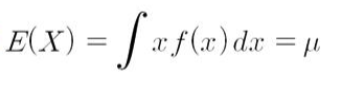
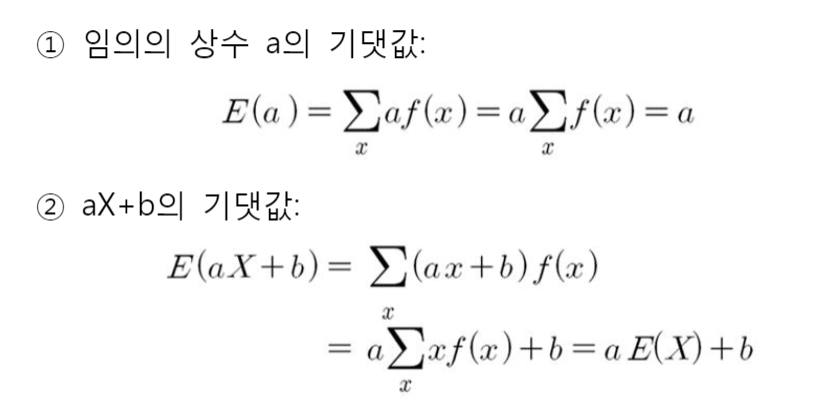
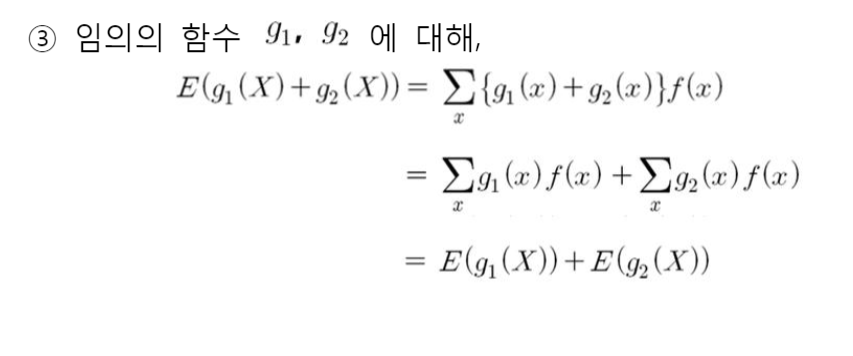
댓글남기기